Expected goals is one of several performance metrics SciSports uses to assess the quality of offensive players. This metric measures the quality of goal-scoring chances and is a better predictor of the number of goals a player is expected to score in the future than traditional statistics like the number of goals, shots and assists. This article first introduces the concept of expected goals and then provides insights into SciSports’ expected-goals metric.
Last updated: 22-10-2018
The expected-goals metric reflects the probability of a given goal-scoring chance to be converted into a goal. Unlike traditional football statistics like the number of shots, the expected-goals metric considers the quality of each goal-scoring chance as well. In doing so, the metric even outperforms the actual number of goals in predicting the number of goals that a player will score in the future. Moreover, the fact that a player’s expected goals is more consistent over time than his actual number of goals makes the expected-goals metric a useful tool in the player recruitment process.
We further explain the concept of expected goals using two illustrative videos. The first video shows a goal attempt by Yakubu in the Nigeria vs South Korea match at the 2010 FIFA World Cup. Yakubu receives the ball in front of an open goal with the goalkeeper already beaten yet still manages to put the ball wide… a near 100% chance wasted! The second video shows a once-in-a-lifetime goal by Zlatan Ibrahimović who scores for Sweden in a friendly against England with a bicycle kick from 30 yards out. While Ibrahimović’s effort goes down in the books as a goal, Yakubu’s miss appears nowhere in the match statistics. However, if both players were offered their goal-scoring chances many times over again, we would expect more goals to arise from Yakubu’s attempt than from Ibrahimović’s.
Intuition behind expected goals
We estimate the expected-goals value for Yakubu’s chance by evaluating the outcomes of a large number of highly similar chances in the past. In particular, we compute the proportion of these similar chances that yields a goal. For example, if 97 out of every 100 similar chances results in a goal, the expected-goals value for Yakubu’s goal attempt is 0.97.
To simplify this example, however, we ignored one crucial question: How do we decide whether two goal-scoring chances are similar or not? Although every goal-scoring chance is unique in its own way, chances often still have many characteristics in common. For example, they occur on roughly the same location on the pitch or the player uses the same body part for his attempt. However, the chances in the videos above were quite different. Yakubu’s attempt was from close range right in front of goal with neither defenders nor goalkeeper between the player and the goal. In contrast, Ibrahimović’s attempt was from far out with several defenders still between the player and the goal. Furthermore, Yakubu’s attempt resulted in a right-footed shot, whereas Ibrahimović’s attempt was the result of a fast counter-attack finished off with a bicycle kick.
An expected-goals model weighs the importance of each relevant characteristic to produce an accurate expected-goals value for each chance. Unsurprisingly, the closer a goal-scoring chance is to the opponent’s goal, the higher its expected-goals value is. Similarly, the tighter the angle between the location of the chance and the goal mouth is, the lower the chance’s expected-goals value is. Furthermore, the model knows that bicycle kicks are harder to convert than right-footed shots and that shots arising from fast counter-attacks lead to goals more often than shots resulting from slow build-up play.
Application in player recruitment
To keep the books in balance, most football clubs need to continuously sell their best players and sign appropriate replacements. The challenge is to sell players who are overvalued by the market and to sign players who are undervalued by the market. In terms of expected goals, players whose actual goal tally outperforms their expected goals are often overvalued and thus interesting players to sell. In contrast, players whose expected goals outperforms their actual number of goals are often undervalued and thus interesting players to buy.
To identify players who perform well on expected goals, we need to take two important considerations into account. The first consideration is to examine a sufficiently large number of goal-scoring chances before drawing conclusions. While expected-goals models might have difficulties to account for the peculiarities of individual goal-scoring chances, these effects cancel out over a large sample of chances. In particular, important information such as the locations of the defenders and the goalkeeper, the number of players in between the shooter and the goal, and the amount of pressure on the shooter might be unknown.
The second consideration is that different types of players excel in converting different types of goal-scoring chances. For example, some players excel in beating the defensive line and dribbling towards goal, whereas other players prefer high crosses into the box. Thus, players who are provided with types of goal-scoring chances they do not favor might score fewer goals than their expected goals suggests. For instance, if Lionel Messi were provided were provided with high crosses instead of low passes, he would likely score less than expected.
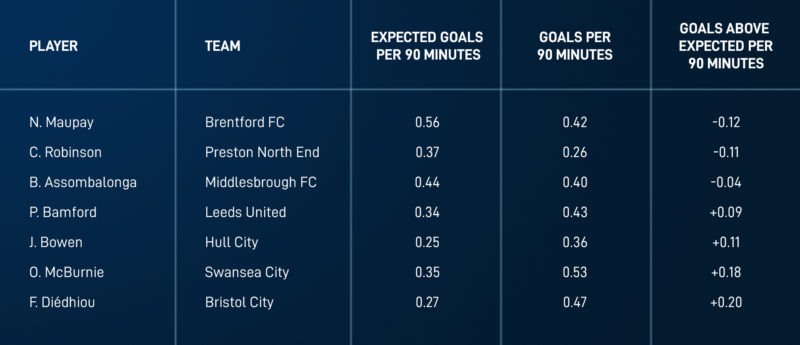
Table 1 lists the expected goals, actual goals and actual goals above expected for seven arbitrarily selected forwards during the 2017/2018 English Championship season. We normalized the statistics per 90 minutes of play to account for differences in the number of minutes played. For example, Neal Maupay of Brentford FC totals 0.56 expected goals and 0.42 actual goals, which yields -0.12 goals above expected per 90 minutes.
Table 1: Expected goals per 90 minutes, actual goals per 90 minutes and goals above expected per 90 minutes for seven arbitrarily selected forwards during the 2017/2018 English Championship season.
As mentioned earlier, players who score fewer goals than their expected-goals tally suggests are interesting to watch. Although Preston North End’s Callum Robinson scored fewer goals than Bristol City’s Famara Diédhiou and Swansea City’s Oliver McBurnie, Robinson seems a more interesting signing based on his expected goals figure. Furthermore, Neal Maupay and Middlesbrough’s Britt Assombalonga are interesting players to watch as well. While both rate high on expected goals per 90 minutes, they lag behind in actual number of goals scored.
In summary, expected goals is a useful performance metric for discovering potentially interesting offensive players. However, it is important to consider other important factors as well such as a player’s general level and a team’s tactical system.
SCISPORTS' PLATFORM
Discover how we use Expected Goals in our player recruitment platform

JOB OPENINGS
We always strive to attract the brightest (tech) talents in the world in order to create technological excellence